Quebra-Cabeça 48 – 45 minutos

A configuração final do tabuleiro vai codificar uma localização dada pela soma NIM de todas as peças brancas.

A soma NIM aplicada a esse quebra-cabeça vai nos dar o seguinte procedimento:

1. Comece com um valor total de 0
2. Verifique as oito peças das linhas 3 e 4: se o número de peças brancas for ímpar, adicione 8 ao valor total
3. Verifique as oito peças das linhas 2 e 4: se o número de peças brancas for ímpar, adicione 4 ao valor total
4. Verifique as oito peças das colunas 3 e 4: se o número de peças brancas for ímpar, adicione 2 ao valor total
5. Verifique as oito peças das colunas 2 e 4: se o número de peças brancas for ímpar, adicione 1 ao valor total

No fim o “valor total” vai ser um número de 0 a 15, que indicará a resposta.

Vamos analisar alguns exemplos.

1. Suponha que a casa escolhida seja a 1 e que o tabuleiro tenha sido deixado com todas as peças viradas com o lado preto para cima. Nesse caso, se você seguir os passos acima verá que a soma NIM deixada no tabuleiro é zero. Preciso mudar a cor de uma das peças para que a soma passe a ser 1. Segundo a regra 5 é necessário mudar uma das peças das colunas 2 e 4 o que nos dará o valor 1, porém, a peça mudada não pode alterar as regras 2, 3, e 4. Isso quer dizer que não podemos alterar valores das linhas 3 e 4 (regra 2), nem da linha 2 (regra 3) e também não da coluna 4 (regra 4). Isso faz com que tenhamos que alterar a peça da própria posição 1, que está na coluna 2 (obedecendo a regra 5) e não fere nenhuma outra regra.
2. Perceba que, no caso do tabuleiro estar todo com peças brancas, a resposta continua sendo a mesma: alterar a peça da casa 1, fazendo a coluna 2 ter um número ímpar de peças brancas.
3. Vamos tomar o exemplo do post (imagem à esquerda). Suponha que ainda seja a casa 1 a escolhida. Pela regra 2 teremos o valor intermediário 8. Pela regra 3 temos 4 que nos dá a soma intermediária 12. Pela regra 4 temos 2 e leva nossa soma intermediária para 14. A regra 5 nos dá um valor 0 e a soma total fica em 14. Precisamos alterar uma casa que esse valor passe a ser 1! Quem nos dá o valor 1 é a regra 5 que envolve as colunas 2 e 4. Perceba que precisamos também zerar as somas das regras 2, 3 e 4. Pelas regras 2 e 3 sabemos que é necessário alterar uma peça da linha 4 que abrange essas duas regras. Para alterar a regra 4 é necessário alterar uma peça da coluna 4, já que se alterarmos a peça da coluna 3 não vamos gerar o valor 1 da regra 5. Ou seja: precisamos alterar a cor da peça da coluna 4 e linha 4, ou seja, a peça 15 vai mudar de branca para preta. 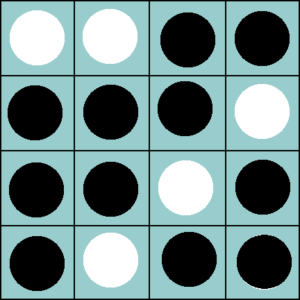Para simplificar o entendimento desse último exemplo, veja a posição final na imagem à direita.Vamos refazer as regras: quantidade de casas brancas nas linhas 3 e 4 é 2, que é par e por isso nos dá valor 0 (regra 2). A quantidade de casas brancas das linhas 2 e 4 é 2, que nos dá novamente valor 0 (regra 3). Temos 2 casas brancas nas colunas 3 e 4 o que nos dá 0 novamente. Por último a soma das casas brancas das colunas 2 e 4 é 3 o que nos dá 1 que somado aos outros zeros continua sendo 1.