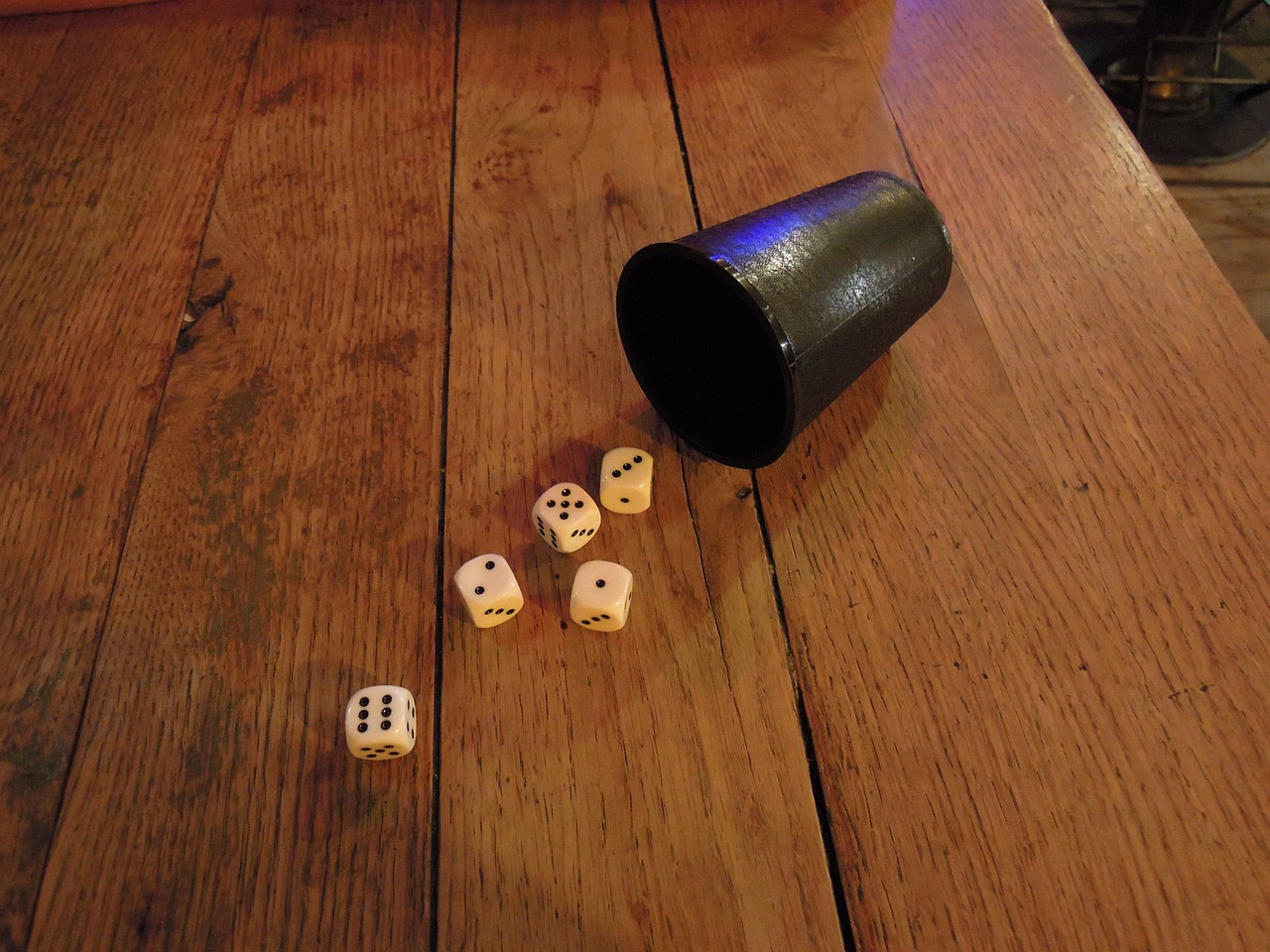Você foi convidado para jogar um jogo de tabuleiro na casa de um amigo. Ao chegar lá vocês começam a retirar as peças da caixa e você se depara com dados de 10 lados. Você nunca tinha visto algo assim e pega nove desses dados os lançando na mesa.
Os dados, estranhamente, param sobre a mesa da seguinte forma:
Antes que você pudesse recolher os dados para jogar novamente seu amigo o impede dizendo:
Olha só! Se você multiplicar o dado que está sozinho no canto esquerdo pela dupla abaixo dele você terá o número do meio! 4 * 38 = 152!
Você acha bastante interessante que isso tenha ocorrido. Antes que pudesse comentar o quão legal seria se a multiplicação do dado mais á direita pela dupla abaixo dele também resultasse no número do meio, seu amigo diz:
Já percebi que é possível rearranjar os dados para que a multiplicação dos números dos cantos pelas respectivas duplas próximas formem o número do meio. Há inclusive mais de uma forma de fazê-lo. Você consegue descobrir qual o número mínimo de dados que devem ser trocados de lugar para que isso ocorra?
Você fica estupefato pois não imaginava que seu amigo pudesse ter enxergado tudo isso tão rápido. A única forma de impressioná-lo é respondendo sua pergunta!
E agora? Como movimentar esses dados?
Confira o resultado oficial no Quebra-Cabeça 27, porém, até lá, fique à vontade para discutir pelos comentários abaixo.
Para descobrir a resposta do Quebra-Cabeça 25 clique na caixa abaixo.