Uma importantíssima máquina de sua fábrica estragou. Depois de chamar diversos profissionais para resolver o problema, e todos falharem, você resolve chamar um “super especialista”. Esse profissional é conhecido por cobrar 1 barra de ouro por dia de trabalho (e dizem que ele não gasta nada do que recebe, só poupa) e além disso ele exige receber ao fim de cada dia.
O trabalho está previsto para 7 dias. Para efetuar o pagamento, você possui 7 barras de ouro, mas elas estão ligadas umas às outras conforme imagem abaixo:
Separar as barras é muito trabalhoso e você pretende fazer o menor número possível de cortes nesse arranjo para efetuar os pagamentos diários.
Qual o número mínimo de cortes que você precisa fazer para efetuar o pagamento diário?
Confira o resultado oficial no Quebra-Cabeça 37, porém, até lá, fique à vontade para discutir pelos comentários abaixo.
Para descobrir a resposta do Quebra-Cabeça 35 clique na caixa abaixo.
Você deve ter percebido que a abordagem de “força bruta” não funciona. Se o camelo tentar levar as 1000 bananas diretamente ao mercado ele vai comer tudo na viagem e não terá bananas para comer na volta.
Precisamos de uma abordagem na qual o camelo deixe as bananas em um ponto intermediário e retorne ao ponto de partida para pegar mais bananas.
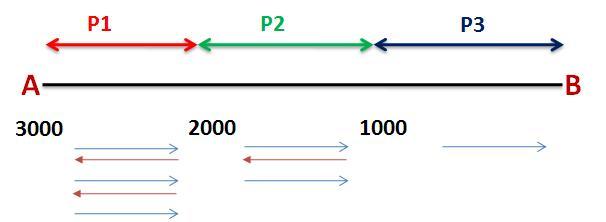
Como temos 3000 bananas e o camelo só consegue levar 1000 por vez ele vai ter que fazer 3 viagens para levar todas as bananas até um ponto intermediário. Vamos chamar esse primeiro trecho de “P1”.
Quando as bananas forem reduzidas a 2000 o camelo só precisará de 2 viagens para levá-las até outro ponto intermediário que chamaremos de “P2”.
Quando só houver 1000 bananas o camelo não precisa mais de pontos intermediários, basta que ele siga adiante.
Na primeira parte, P1, para percorrer 1km com todas as bananas o camelo terá que:
1. Andar 1km com 1000 bananas (comendo 1 banana nessa ida) 2. Deixar 998 bananas nesse ponto e retornar com 1 banana (comendo essa 1 banana) 3. Pegar as próximas 1000 bananas e seguir adiante (comendo 1 banana nessa nova ida) 4. Deixar 998 bananas nesse ponto e retornar com 1 banana (comendo essa 1 banana) 5. Carregar as últimas 1000 bananas do ponto A ao ponto intermediário (comendo 1 banana)
Depois do passo 5 o camelo não precisa mais voltar ao ponto de partida (o ponto A).
Com isso temos que para andar 1km com as 3000 bananas o camelo vai comer 5 bananas.
Depois de andar 200 km o camelo teria comido 1000 bananas e ficaria agora com apenas 2000 bananas.
Portanto a distância “P1” é de 200 Km.
Agora, para percorrer o trecho P2, o Camelo precisa fazer o seguinte para andar 1km com as bananas:
1. Levar 1000 bananas ao novo ponto intermediário (comendo 1 banana no caminho) 2. Deixar 998 bananas nesse ponto e retornar com 1 banana (comendo 1 banana nessa volta) 3. Pegar as 1000 bananas restantes e seguir em frente (comendo 1 banana no caminho)
Depois do passo 3 o camelo não precisa mais retornar ao início do trecho P2.
Com isso temos que para andar 1km com as 2000 bananas o camelo vai comer 3 bananas.
Depois de percorrer 333.3 km o camelo teria comido 1000 e 1/3 bananas, ficando apenas com 999 e 2/3.
Portanto a distância “P3” é de 333.3 Km.
Agora, para o trecho “P3”, o camelo só tem que levar as “999 + 2/3” bananas direto ao ponto B, sem usar paradas intermediárias. Ele já viajou 533.3 km (200+333.3) dos 1000 km. Agora ele tem que percorrer só 466.7 km.
Ele vai comer 466 bananas e 2/3, durante esse último trecho e chegará ao ponto B com 533 bananas.
Gostou desse quebra-cabeça?
Baixe agora um ebook com dezenas de quebra-cabeças já postados aqui no site! É gratuito!
Pode ficar tranquilo: não compartilharemos seu email com ninguém!
